|
| (4 comments) | 15.059 times displayed |
 |
Un cerc cu centrul in E, e "prins la mijloc" de un hexagon mare si un alt hexagon mic, ca in imagine, adică în hexagonul regulat mare este inscris cercul care la rândul său este circumscris altui hexagon regulat cu lungimea laturii mai mică.
Dacă hexagonul înscris are aria de 3 m pătra?i, care e aria hexagonului exterior ? |
|
|
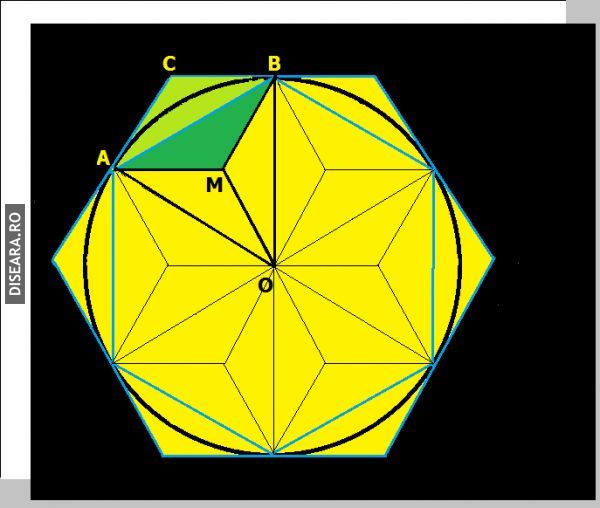 Se rotește cercul în care e înscris hexagonul mic până când vârfurile hexagonului vor fi tangente hexagonului mare. Se împarte hexagonul interior in șase triunghiuri echilaterale (egale cu AOB),iar acestea se împart în câte trei triunghiuri isoscele egale (AMB, M fiind centrul de greutate al triunghiului ABO. Acum e clar că aria triunghiului ABC din hexagonul exterior, este egală cu cea a unui triunghi isoscel (AMB). De aici rezultă imediat că hexagonul exterior are aria egală cu 4 m pătrați. |
Today's Problem
Top 10 most viewed problems