|
| (7 comentarii) | 6.636 afisari |
 |
Fie un triunghi ABC in care
u(CAB) < u(BCA) < 90° < u(ABC)
unde u(CAB) este unghiul A al triunghiului, etc. Fie AM bisectoarera unghiului exterior triunghiului in A, cu M apartinand dreptei BC. Fie BN bisectoarea unghiului exterior triunghiului in B, cu N apartinand dreptei AC. Sa se calculeze u(CAB) stiind ca:
AM = BN = AB |
|
|
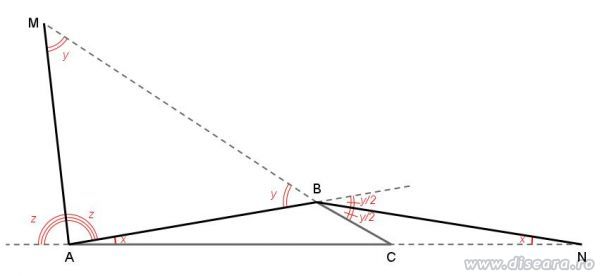 In figura sunt notate unghiurile egale datorata trunghiurilor isoscele:
- x in triunghiul ABN (AB=BN)
- y in triunghiul MAB (MA=AB)
si unghiurile egale datorita bisectoarelor:
- z in unghiul exterior in A al triunghiului ABC
- y/2 in unghiul exterior in B al triunghiului ABC
Cu aceste unghiuri se pot construi relatii. Suma unghiurilor din jurul punctului A da:
x + 2z + 180° = 360°
In triunghiul ABM suma unghiurilor in triunghi da:
2y + z = 180°
In triunghiul ABN suma unghiurilor in triunghi da:
2x + 180° - y + y/2 = 180°
Rezulta deci sistemul de 3 ecuatii cu 3 necunoscute:
x + 2z = 180°
2y + z = 180°
4x - y = 0°
cu solutiile:
x = 12°
y = 48°
z = 84° |

