Un triunghi cât un pătrat |
Propusă de
lucipet |
|
| (4 comentarii) | 2.587 afisari |
 |
In figura alăturată au fost desenate cinci pătrate cu lungimile laturilor diferite. Arătați că aria suprafeței triunghiului mărginit de laturile celor mai mari pătrate (triunghiul verde), este egală cu aria pătratului cu laturile colorate în roșu . |
|
|
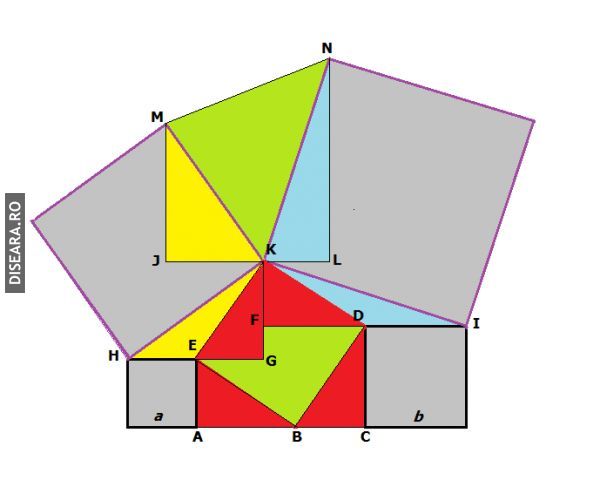 Construim prin K paralela JL la laturile HE si DI, apoi MJ și NL perpendiculare pe JL.Ducem KG ḻ HE in G si KF ḻ DI in F , deci MJ paralela cu NL . Fie a și b lungimile laturilor celor mai mici pătrate . Δ MJK = Δ HKG (au ipotenuzele egale și unghiurile adiacente au laturile perpendiculare – ex. unghiul KMJ = unghiul KHG).Similar se arată ca Δ KLN = Δ KFI.Se mai observă că Δ ABE = Δ BCD din motive similare, iar Δ EKG = Δ KDF. De remarcat și faptul ca S HEK = S EKG (KE este mediană și împarte Δ-ul în câte două Δ-uri cu suprafețe echivalente (cu aceeași arie). Similar KD mediană în Δ KFI (toate triunghiurile roșii sunt egale).
In aceste condiții , cum trapezul JLNM este dreptunghic, avem
S(KNM) = S(JLNM) – S(MJK) – S(KLN) = (2a + 2b)(b+a)/2 – (2a *b)/2 – (2b*a)/2 = (a + b)2 – 2ab = a2 + b2 = EB2 = S(EBDK).
(a = BC , b = AB). Deci ariile celor 2 suprafețe sunt egale.
( S(XYZ) inseamna aria poligonului XYZ ) |
|
|
Tags:
|
problema zilei,
probleme de matematica,
amuzante,
matematica amuzanta,
probleme rezolvate,
solutii,
rezolvari,
geometrie
|
|
|
| Probleme similare: |
|
intrebare,
Final de an la clasa a...,
geometrie,
Unghiul albastru,
problema dubla,
problema 8,
Reordine,
12 cifre pe cuburi,
Probleme concurs clasa 5,
Ceva simplu, accesibil...,
Cât este distanța între...,
Cîte pătrate?,
suma si produs,
Patrat cu probleme.,
Culoarea și numarul de...,
Cele trei comori din...,
Ce face al şaptelea...,
Sens unic,
3 zaruri,
... și un alt pătrat
|
|
|
Problema zilei
Top 10 cele mai văzute probleme