|
|

|
Luni, 25 ianuarie 2010 |

|
|
|
SARITURI FARA ... OBSTACOLE |
Propusă de
lucipet |
|
| (17 comentarii) | 8.456 afisari |
 |
Diagrama din stanga , extrasa de pe un sait de jocuri al unui fan diseara.ro, demonstreaza cum un cal sare prin toate cele 64 de campuri ale tablei de sah pornind de pe a1 pana la a8 , trecand o singura data prin fiecare camp.
Se poate gasi un traseu , de data asta pentru calul din h1 in diagrama din dreapta, care sa treaca o singura data prin fiecare camp al tablei si sa ajunga pe campul a8 ? |
|
|
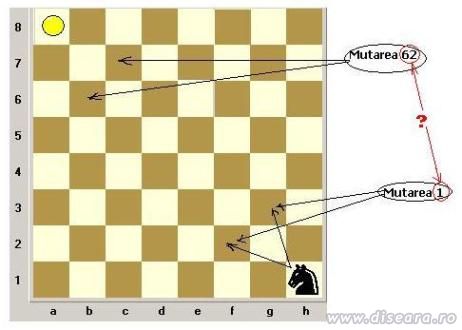 Orice mutare a calului pe tabla de sah il duce pe acesta pe un camp de culoare diferita de cea a campului de pe care a plecat. Pentru a ajunge pe al N-lea camp , se efectueaza N-1 mutari. Initial , calul se gasea pe un camp alb. La mutarea cu numarul 1, deci la o mutare impara, calul ajunge pe un camp negru, la a doua pe unul alb,la a treia pe unul negru si asa mai departe. Toate mutarile de rang impar duc calul pe camp negru iar cele de rang par, pe unul alb. Pozitia calului inainte de a 63-a mutare, care e ultima, gaseste calul pe un camp negru. Ar rezulta ca mutarea a 62-a ,adica una de rang par, ar fi adus calul pe un camp negru,lucru care ar intra in contradictie cu cele de mai sus. Rezulta ca nu exista un traseu pe care sa-l parcurga un cal de la h1 la a8 pe tabla de sah . |
|
|
|
|
|
 |
Caută probleme după cuvinte cheie
|
|
|
|
 |
|
|
|
|
|
|
|

