|
|
|
Marţi, 2 septembrie 2008 |
|
|
|
Unde pică bila? |
Propusă de
bazil |
|
| (9 comentarii) | 6.725 afisari |
 |
Într-un joc, o bilă poate avea 5 poziţii: 1, 2, 3, 4, 5. Schimbarea poziţiei bilei, la impulsul jucătorului, este supusă următoarelor restricţii:
(a) - bila poate ajunge în 1 doar plecând din 5;
(b) - bila poate ajunge în 2 doar plecând din 3;
(c) - bila poate ajunge în 3 doar plecând din 4;
(d) - bila poate ajunge în 4 plecând din 1 sau 2;
(e) - bila poate ajunge în 5 plecând din 2 sau 3;
(f) - bila nu poate rămâne pe loc la impulsurile jucătorului;
(g) - iniţial bila este în poziţia 1.
Care este numărul minim de impulsuri ce se pot aplica bilei, astfel încât bila să revină în poziţia 1? Dar numărul maxim de impulsuri? |
|
|
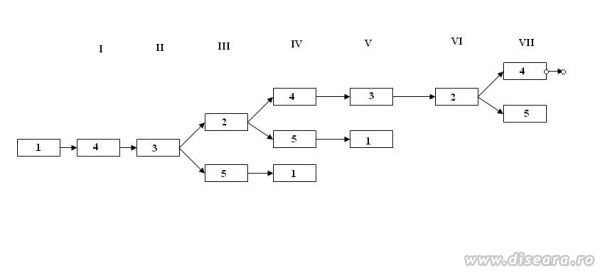 O rezolvare grafică este reprezentată alăturat.
Numărul minim de impulsuri se obţine pe ramura de jos, respectiv secvenţa:
1 -> 4 -> 3 -> 5 -> 1, adică 4 impulsuri.
Numărul maxim de impulsuri se obţine pe ramura de sus, care este infinită:
1 -> 4 -> 3 -> 2 -> 4 -> 3 -> 2 etc. Adică în această situaţie bila nu mai revine în poziţia 1. |
|
|
|
|
|
 |
Caută probleme după cuvinte cheie
|
|
|
|
|
|
|
|
|
|
|
|
Problema zilei
Top 10 cele mai văzute probleme